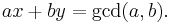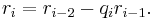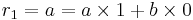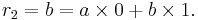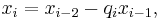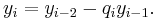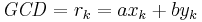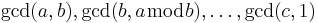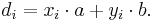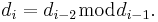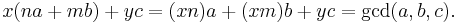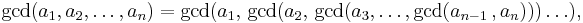Extended Euclidean algorithm
The extended Euclidean algorithm is an extension to the Euclidean algorithm. Besides finding the greatest common divisor of integers a and b, as the Euclidean algorithm does, it also finds integers x and y (one of which is typically negative) that satisfy Bézout's identity
The extended Euclidean algorithm is particularly useful when a and b are coprime, since x is the multiplicative inverse of a modulo b, and y is the multiplicative inverse of b modulo a.
Contents |
Informal formulation of the algorithm
| Dividend | Divisor | Quotient | Remainder |
|---|---|---|---|
| 120 | 23 | 5 | 5 |
| 23 | 5 | 4 | 3 |
| 5 | 3 | 1 | 2 |
| 3 | 2 | 1 | 1 |
| 2 | 1 | 2 | 0 |
To illustrate the extension of Euclid's algorithm, consider the computation of gcd(120, 23), which is shown on the table on the left. Notice that the quotient in each division is recorded as well alongside the remainder.
In this case, the remainder in the fourth line (which is equal to 1) indicates that the gcd is 1; that is, 120 and 23 are coprime (also called relatively prime). For the sake of simplicity, the example chosen is a coprime pair; but the more general case of gcd other than 1 also works similarly.
There are two methods to proceed, both using the division algorithm, which will be discussed separately.
Iterative method
This method computes expressions of the form 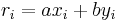 for the remainder in each step
for the remainder in each step  of the Euclidean algorithm. Each successive number
of the Euclidean algorithm. Each successive number 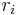 can be written as the remainder of the division of the previous two such numbers, which remainder can be expressed using the whole quotient qi of that division as follows:
can be written as the remainder of the division of the previous two such numbers, which remainder can be expressed using the whole quotient qi of that division as follows:
By substitution, this gives:
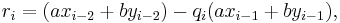 which can be written
which can be written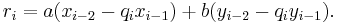
The first two values are the initial arguments to the algorithm:
So the coefficients start out as x1 = 1, y1 = 0, x2 = 0, and y2 = 1, and the others are given by
The expression for the last non-zero remainder gives the desired results since this method computes every remainder in terms of a and b, as desired.
Example: Compute the GCD of 120 and 23.
The computation proceeds as follows:
| Step | Quotient | Remainder | Substitute | Combine terms | |
|---|---|---|---|---|---|
| 1 | 120 | 120 = 120 × 1 + 23 × 0 | |||
| 2 | 23 | 23 = 120 × 0 + 23 × 1 | |||
| 3 | 5 | 5 = 120 − 23 × 5 | 5 = (120 × 1 + 23 × 0) − (120 × 0 + 23 × 1) × 5 | 5 = 120 × 1 + 23 × −5 | |
| 4 | 4 | 3 = 23 − 5 × 4 | 3 = (120 × 0 + 23 × 1) − (120 × 1 + 23 × −5) × 4 | 3 = 120 × −4 + 23 × 21 | |
| 5 | 1 | 2 = 5 − 3 × 1 | 2 = (120 × 1 + 23 × −5) − (120 × −4 + 23 × 21) × 1 | 2 = 120 × 5 + 23 × −26 | |
| 6 | 1 | 1 = 3 − 2 × 1 | 1 = (120 × −4 + 23 × 21) − (120 × 5 + 23 × −26) × 1 | 1 = 120 × −9 + 23 × 47 | |
| 7 | 2 | 0 | End of algorithm | ||
The last line reads 1 = 120 × −9 + 23 × 47, which is the required solution: x = −9 and y = 47.
Since the GCD turns out to be 1, this also means that 47 gives the multiplicative inverse of 23 in modulo 120, and also that in modulo 23, −9 (or 14, which represents the same element) gives the multiplicative inverse of 120 (or equivalently of 5).
- 47 × 23 ≡ 1 (mod 120) and also −9 × 120 ≡14 × 5 ≡ 1 (mod 23).
For an integer a to be invertible modulo b, it is necessary that a and b be coprime, so if a GCD greater than 1 is found, one may conclude that such a modular inverse does not exist.
Note that the equations defining the values xi are independent of those defining the values yi, and that the Bézout identity found at the end
allows deducing yk when xk is known. One can therefore omit the values yi from the computation (although they can be useful to check for computational errors). This is particularly relevant for applications, such as computing modular inverses, that require the value of only one Bézout coefficient.
Recursive method
This method attempts to solve the original equation directly, by reducing the dividend and divisor gradually, from the first line to the last line, which can then be substituted with trivial value and work backward to obtain the solution.
Consider the original equation:
| 120 | x | + | 23 | y | = | 1 |
| (5×23 + 5) | x | + | 23 | y | = | 1 |
| 23 | (5x + y) | + | 5 | x | = | 1 |
| ... | ||||||
| 1 | xk | + | 0 | yk | = | 1 |
Notice that the equation remains unchanged after decomposing the original dividend in terms of the divisor plus a remainder, and then regrouping terms. If we have a solution to the equation in the second line, then we can work backward to find x and y as required. Although we don't have the solution yet to the second line, notice how the magnitude of the terms decreased (120 and 23 to 23 and 5). Hence, if we keep applying this, eventually we'll reach the last line, which obviously has (1, 0) as a trivial solution. Then we can work backward and gradually find out x and y.
| Dividend | = | Quotient | x | Divisor | + | Remainder |
|---|---|---|---|---|---|---|
| 120 | = | 5 | x | 23 | + | 5 |
| 23 | = | 4 | x | 5 | + | 3 |
| ... | ||||||
For the purpose of explaining this method, the full working will not be shown. Instead some of the repeating steps will be described to demonstrate the principle behind this method.
Start by rewriting each line from the first table with division algorithm, focusing on the dividend this time (because we'll be substituting the dividend).
| 120 | x0 | + | 23 | y0 | = | 1 |
| (5×23+5) | x0 | + | 23 | y0 | = | 1 |
| 23 | (5x0+y0) | + | 5 | x0 | = | 1 |
| 23 | x1 | + | 5 | y1 | = | 1 |
| (4×5+3) | x1 | + | 5 | y1 | = | 1 |
| 5 | (4x1+y1) | + | 3 | x1 | = | 1 |
| 5 | x2 | + | 3 | y2 | = | 1 |
|
Table method
The table method, also known as "The Magic Box", is probably the simplest method to carry out with a pencil and paper. It is similar to the iterative method, although it does not directly require algebra to use. The main idea is to think of the equation chain
as a sequence of divisors 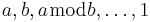 . In the running example we have the sequence 120, 23, 5, 3, 2, 1. Any element in this chain can be written as a linear combination of the original
. In the running example we have the sequence 120, 23, 5, 3, 2, 1. Any element in this chain can be written as a linear combination of the original  and
and  , most notably, the last element,
, most notably, the last element, 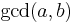 , can be written in this way. The table method involves keeping a table of each divisor, written as a linear combination. The algorithm starts with the table as follows:
, can be written in this way. The table method involves keeping a table of each divisor, written as a linear combination. The algorithm starts with the table as follows:
-
x y d 1 0 120 0 1 23
The elements in the  column of the table will be the divisors in the sequence. Each
column of the table will be the divisors in the sequence. Each 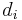 can be represented as the linear combination
can be represented as the linear combination
The  and
and  values are obvious for the first two rows of the table, which represent
values are obvious for the first two rows of the table, which represent  and
and  themselves. To compute
themselves. To compute 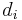 for any
for any 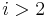 , notice that
, notice that
Suppose 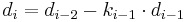 . Then it must be that
. Then it must be that
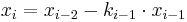 and
and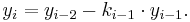
This is easy to verify algebraically with a simple substitution.
Actually carrying out the table method though is simpler than the above equations would indicate. To find the third row of the table in the example, just notice that 120 divided by 23 goes 5 times plus a remainder. This gives us k, the multiplying factor for this row. Now, each value in the table is the value two rows above it, minus k times the value immediately above it. This correctly leads to
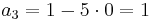 ,
,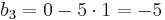 , and
, and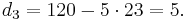
After repeating this method to find each line of the table (note that the remainder written in the table and the multiplying factor are two different numbers!), the final values for  and
and  will solve
will solve 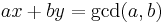 :
:
-
x y d k 1 0 120 0 1 23 5 1 -5 5 4 -4 21 3 1 5 -26 2 1 -9 47 1 2
This method is simple, requiring only the repeated application of one rule, and leaves the answer in the final row of the table with no backtracking. Note also that if you are intending to find a modular inverse for a modulo b and you end up with x being negative, you then need to add the modulus b to x in order to bring it into the range 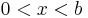 . This does not affect the validity of the solution as we have
. This does not affect the validity of the solution as we have 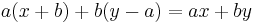 .
.
Formal description of the algorithm
Iterative method
By routine algebra of expanding and grouping like terms (refer to last section), the following algorithm for iterative method is obtained:
- Apply Euclidean algorithm, and let qn(n starts from 1) be a finite list of quotients in the division.
- Initialize x0, x1 as 1, 0, and y0, y1 as 0,1 respectively.
- Then for each i so long as qi is defined,
- Compute xi+1 = xi−1 − qixi
- Compute yi+1 = yi−1 − qiyi
- Repeat the above after incrementing i by 1.
- The answers are the second-to-last of xn and yn.
Pseudocode for this method is shown below:
function extended_gcd(a, b)
x := 0 lastx := 1
y := 1 lasty := 0
while b ≠ 0
quotient := a div b
(a, b) := (b, a mod b)
(x, lastx) := (lastx - quotient*x, x)
(y, lasty) := (lasty - quotient*y, y)
return (lastx, lasty)
Extra steps are needed when working with negative a and/or b.
Recursive method
Solving the general case of the equation in the last corresponding section, the following algorithm results. Given any pair of nonnegative integers a, b, it finds integers values x, y such that ax + by is nonnegative and divides both a and b, which implies that it is the greatest common divisor of a and b.
- If b = 0, the algorithm ends, returning the solution x = 1, y = 0.
- Otherwise:
- Determine the quotient q and remainder r of dividing a by b using the integer division algorithm.
- Then recursively find coefficients s, t such that bs + rt divides both b and r.
- Finally the algorithm returns the solution x = t, and y = s − qt.
This can be written in pseudocode as follows:
function extended_gcd(a, b)
if b = 0
return (1, 0)
else
(q, r) := divide (a, b)
(s, t) := extended_gcd(b, r)
return (t, s - q * t)
This assumes a "divide" procedure exists that returns a (quotient,remainder) pair (one could alternatively put q := a div b, and then r = a − b * q).
Proof of correctness
Let a and b be nonnegative integers. We wish to prove that the algorithm terminates, and returns (x, y) such that ax + by divides both a and b. We proceed by induction on b.
- If b = 0, then the algorithm terminates immediately with x = 1 and y = 0, so ax + by = a; this is clearly nonnegative and divides both a and 0 (as 0a = 0).
- Otherwise let q, r be obtained from the division of a by b as in the algorithm description, so a = bq + r and r < b by the properties of the division algorithm.
- The inequality r < b means we can apply the induction hypothesis for (b,r) in the place of (a,b), and this guarantees that the recursive application terminates.
- Let (s,t) be the values it returns; by induction we know that bs + rt is nonnegative and divides both b and r.
- Now the algorithm returns x = t and y = s − qt. We have ax + by = at + b(s − qt) = bs + (a − bq)t = bs + rt, which is (still) nonnegative and divides both b and r. The same number therefore also divides r + bq = a, which terminates the proof.
The proof shows that the recursive algorithm can be adapted to deal with arbitrary integers a, b with just a slight modification: in the terminating case b = 0 it should test the sign of a, and if it is negative return x = −1 instead of x = 1, to ensure that ax + by is always nonnegative. This does assume that the division algorithm works if a and/or b are negative, and ensures that |r| < |b| in all cases (the usual specification of the division algorithm in fact requires r to be nonnegative, but this is not necessary in the proof, which is now by recurrence on |b|).
Computing a multiplicative inverse in a finite field
The extended Euclidean algorithm can also be used to calculate the multiplicative inverse in a finite field.
Pseudocode
Given the irreducible polynomial f(x) used to define the finite field, and the element a(x) whose inverse is desired, then a form of the algorithm suitable for determining the inverse is given by the following. NOTE: remainder() and quotient() are functions different from the arrays remainder[ ] and quotient[ ]. remainder() refers to the remainder when two numbers are divided, and quotient() refers to the integer quotient when two numbers are divided. Division (with remainder) must be calculated in terms of polynomial arithmetic and not as with "normal" numbers.
remainder[1] := f(x)
remainder[2] := a(x)
auxiliary[1] := 0
auxiliary[2] := 1
i := 2
while remainder[i] > 1
i := i + 1
remainder[i] := remainder(remainder[i-2] / remainder[i-1])
quotient[i] := quotient(remainder[i-2] / remainder[i-1])
auxiliary[i] := -quotient[i] * auxiliary[i-1] + auxiliary[i-2]
inverse := auxiliary[i]
Note
The minus sign is not necessary for some finite fields in the step.
auxiliary[i] := -quotient[i] * auxiliary[i-1] + auxiliary[i-2]
This is true since in the finite field GF(28), for instance, addition and subtraction are the same. In other words, 1 is its own additive inverse in GF(28). This occurs in any finite field GF(2n), where n is an integer.
Example
For example, if the polynomial used to define the finite field GF(28) is f(x) = x8 + x4 + x3 + x + 1, and x6 + x4 + x + 1 = {53} in big-endian hexadecimal notation, is the element whose inverse is desired, then performing the algorithm results in the following:
| i | remainder[i] | quotient[i] | auxiliary[i] |
|---|---|---|---|
| 1 | x8 + x4 + x3 + x + 1 | 0 | |
| 2 | x6 + x4 + x + 1 | 1 | |
| 3 | x2 | x2 + 1 | x2 + 1 |
| 4 | x + 1 | x4 + x2 | x6 + |
| 5 | 1 | x + 1 | x7 + x6 + x3 + |
- Note: Addition in a binary finite field is XOR.
Thus, the inverse is x7 + x6 + x3 + x = {CA}, as can be confirmed by multiplying the two elements together.
The case of more than 2 numbers
One can handle the case of more than 2 numbers iteratively. First we show that 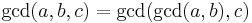 . To prove this let
. To prove this let 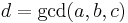 . By definition of gcd
. By definition of gcd  is a divisor of
is a divisor of  and
and  . Thus
. Thus 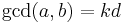 for some
for some  . Similarly
. Similarly  is a divisor of
is a divisor of  so
so 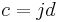 for some
for some  . Let
. Let 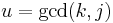 . By our construction of
. By our construction of  ,
, 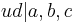 but since
but since  is the greatest divisor
is the greatest divisor  is a unit. And since
is a unit. And since 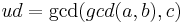 the result is proven.
the result is proven.
So if  then there are
then there are  and
and  such that
such that 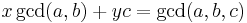 so the final equation will be
so the final equation will be
So then to apply to n numbers we use induction
with the equations following directly.
See also
References
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Pages 859–861 of section 31.2: Greatest common divisor.
External links
|
|||||||||||||||||||||||||||||